For anyone who has been watching the AI landscape over the last decade, the explosion in popularity in deep neural networks (DNNs) has been incredible to watch. DNNs have become the models of choice for an ever-increasing range of application spaces and have delivered State-of-the-Art results in every space into which they are deployed. In the Natural Language Processing (NLP) space, the introduction of transformers has been nothing short of transformational (sorry, pun intended).
However, this revolution has not been without cost. These DNN models are often incredibly complex, and it takes significant computational resources to both train and deploy these models. And these resulting costs are real; both in terms of cloud costs, and the cost to the planet from the associated energy consumption. For example, training the original BERT-large model took 64 TPU chips running for 4-days. At a cost of around $7000 and a not inconsiderable use of power!
And, since the introduction of the BERT, costs have only increased. As companies continue to improve model performance, model complexity is increasing exponentially. The original BERT-large model has 350 million parameters, the much-discussed GPT3 model has 175 billion parameters, and Google announced earlier this year it had trained a 1.6 trillion parameter model! That’s over a 4000X increase in just a few years. This is clearly unsustainable! Surely, we can be smarter about how we achieve this progress, rather than attempting to ‘brute force’ solutions with bigger and bigger compute clusters?
Numenta’s Neuroscience Approach to Sparsity
At Numenta, we have studied the brain’s neocortex for the last 15-years, and we believe that our highly efficient brains provide inspiration for how to deliver transformational changes in AI. While our brains are poorly suited to multiplying 64-bit numbers, they are easily able to outperform cutting-edge AI implementations for practically all real-world learning tasks. And we do so using less than 20W of power! Through our neuroscience research, we’ve figured out how to apply the principles of the brain to machine learning systems and achieve breakthrough performance. We recently released a Whitepaper discussing how we can leverage a couple of these brain-derived insights to, not only improve the performance of a standard DNN by over 100X, but do so while delivering a 100X reduction in the power used to compute each prediction!
While a human neocortex has around 20 billion neurons, at any given moment only a small fraction of the brain’s neurons are active, and individual neurons are only interconnected with a small fraction of the total neurons in the brain. By leveraging this sparsity, the brain is able to control its compute costs. This in stark contrast to contemporary DNNs, where the neurons at each layer are typically connected to every neuron in the previous layer, and all neurons are considered active.
Applying Sparsity without Sacrificing Accuracy
We can leverage these neuroscience insights and introduce sparsity into DNN models; by aggressively limiting the interconnectedness of the neurons and limiting the number of neurons that can be simultaneously activated. And, while it may seem counterintuitive at first glance, we can do so without sacrificing model accuracy! In fact, when done correctly, it can be possible to reduce interconnectedness by 95% while retaining the accuracy of the original ‘dense’ model. Similarly, neuron activations can be limited to around only 10%. While interest in sparsity in the AI community has increased in recent years, Numenta’s techniques are based on inspiration from neuroscience and aim for levels of sparsity that are much higher than what is typically seen in the deep learning literature.
When computing the output of a standard dense DNN model, the output of each neuron must be calculated by computing the weighted sum of all of the inputs to the neuron. These inputs are typically the outputs of the neurons in the prior layer of the model. And in a standard dense layer, each neuron is connected to all of the neurons in the prior layer i.e., if there are 1024 neurons in layer 1, each neuron in layer 2 has 1024 inputs! It’s then necessary to move through the model layer by layer, computing the outputs from the Nth layer, based activity of the N-1th layer, until outputs from the final layer of neurons are computed. As can be readily imagined, computing even a single prediction involves significant computational cost. Similarly, it should be apparent that introducing sparsity significantly reduces the number of computations required. And the benefits of weight and activation sparsity are multiplicative; if a neuron is only connected to 10% of the neurons in the prior layer, and if only 10% of the prior layer’s neurons are activated, the number of computations could be reduced by 100X compared to a standard fully connected dense layer!
Today’s Hardware Constraints
Given the seemingly incredible efficiency benefits that can be derived from sparse models, why is such an approach not common/mandatory in AI? Unfortunately, it is surprisingly difficult to realize the potential efficiency gains of sparse models on today’s commodity hardware.
Modern CPUs and GPUs often boast incredible compute performance numbers, delivering multiple TFLOPs or over one million floating operation arithmetic operations per second. However, to approach these performance numbers outside of carefully crafted benchmarks there is a need for predictable memory access patterns and dense data packing. This enables the full use of a processor’s data prefetchers to load the data in a timely manner and ensures that the vector units can perform multiple operations in parallel.
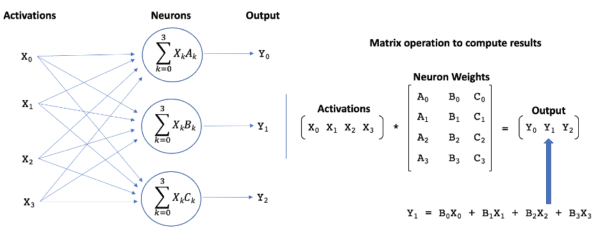
When every neuron in a layer is fully connected to every neuron in the prior layer, the computation of the outputs from the neurons can be formulated as a matrix multiplication operation, as illustrated in Figure 1. The matrix contains the neural weights associated with each neuron in layer N, and the vector is the outputs (aka activations) from the prior layer (N-1) of neurons. These dense matrix math operations are a perfect match for today’s hardware, and the importance of matrix operations across a wide variety of application domains has ensured that processor architectures and associated software are highly optimized for these operations.
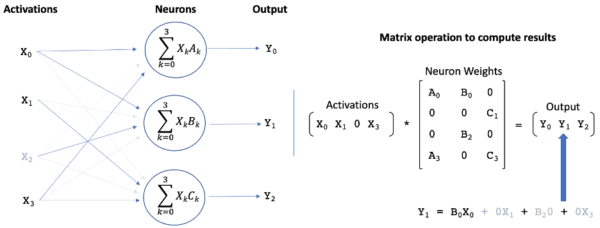
Reducing the interconnectedness of the neurons sets many of the elements in the weight matrix to zero, as illustrated in Figure 2. Similarly, limiting activations sets many elements in the activation vector to zero. Given that multiplication by zero results in a zero-valued product, the introduction of sparsity should allow a significant reduction in the number of computations required to compute the matrix multiplication. However, because sparsification techniques attempt to remove the least important weights in the network, the zero values are typically scattered randomly throughout the matrix, making it is surprisingly difficult for modern CPUs and GPUs to efficiently take advantage of their presence. For example, on a CPU a ‘random’ sparsity of over 90% might be required to achieve a just 2X performance improvement over a standard matrix multiplication operation.
Unlocking Performance Gains with FPGAs
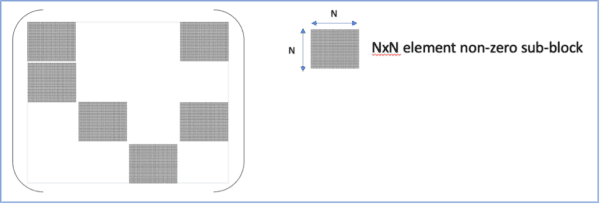
We can attempt to force the placement of the non-zero matrix values to enable improved performance on these architectures. For instance, grouping the non-zero values into sub-blocks within the matrix provides a regular dense sub-structure that is more compatible with contemporary architectures, as illustrated in Figure 3. However, placing constraints on the locations of the zero-elements rapidly begins to impact the achievable accuracy of the sparse model. What is required is the pairing of a flexible architecture with lightweight connectivity and activation constraints. In this whitepaper, we demonstrate that such a flexible architecture is readily available today in the form of Field-Programmable Gate Arrays (FPGAs)!
FPGAs are unlike modern CPUs and GPUs. They are based around a matrix of configurable logic blocks that are connected via programmable interconnects. These configurable blocks are typically complemented by DSPs, and, in some instances, even small, embedded processors. This configurability facilitates efficient sparse network implementations that are fully able to capitalize on the presence of zero-valued weights and activations.
In the whitepaper, we take a convolutional neural network (CNN) that has been trained to classify the short-spoken utterances that are part of the Google speech commands dataset and compare the performance (in terms of inference operations per second) of the standard dense version of this CNN against sparse implementations of the same network on two Xilinx FPGA platforms. The two FPGAs were chosen to highlight the wide spectrum of FPGAs solutions available, with the first being a high-end data-center accelerator card, and the second being a power-constrained solution that represents an ideal platform for “AI-at-the-edge” deployments.
Sparse-Sparse Techniques
In the Whitepaper, we also highlight the performance of two varieties of the sparse model. The first, termed sparse-dense, is focused on weight sparsity and ignores the potential benefits of sparse activations. The second, termed sparse-sparse, leverages both weight sparsity and activation sparsity. The rationale for developing both varieties was two-fold. Firstly, to showcase the relative performance contributions of the different forms of sparsity. Secondly, deriving performance benefits from activation sparsity is significantly less commonplace than leveraging weight sparsity: while the location of the non-zero weights might be random, the locations are nevertheless fixed once training is completed, while the location of the non-zero activations is input dependent and is fluid during inference.
The sparse CNN networks have an overall weight sparsity of around 95%, although the per-layer sparsity varies significantly for accuracy considerations. Activation sparsity is around 90%. The sparse implementations of the CNN are found to not only outperform their dense counterparts by a significant margin, but also leverage significantly fewer FPGA resources. The reduced resource utilization allows additional copies of the network to be accommodated on the FPGA, and processing is load-balanced across the individual copies.
For the data center FPGA card, we found that the standard industry tools could place 4 copies of the dense network on the FPGA, for a combined inference performance of 12K samples per second. In contrast, for the sparse-dense network, the FPGA could accommodate 24 copies delivering a combined inference performance of 689K samples per second. This represents a 56X improvement in inference performance by leveraging weight sparsity! For the sparse-sparse network, the FPGA could accommodate 20 copies of the network, with a combined inference performance of 1.3M samples per second. This represents a 112X improvement compared with the dense network baseline, and a 2X improvement over the sparse-dense implementation!
Reducing Power Consumption
In addition to the impressive performance improvements, the sparse implementations also deliver a corresponding reduction in power consumption; leveraging the same FPGA resources and consuming the same power as the dense baseline, they use this same power budget to perform two orders of magnitude more inference operations.
Switching attention to the power-constrained edge solution, a performance comparison with the dense network is not possible. The dense network is too large to even fit on this FPGA! However, not only was it possible to accommodate both the sparse-dense and sparse-sparse implementations, allowing sophisticated deep neural networks to be run at the edge, the sparse networks on this card also outperformed the dense networks running on the high-end data center card by 3.7X, further highlighting the potential of sparse networks!
Conclusion
In conclusion, as both the monetary and environmental costs of AI continue to increase precipitously, Numenta has clearly demonstrated that, by applying insights from neuroscience, significant performance and efficiency gains can be achieved. In our recent Whitepaper, we demonstrate that by coupling Numenta’s techniques for training extremely sparse networks with flexible hardware architectures, such as FPGAs, a performance improvement of over two orders of magnitude can be achieved. And this performance improvement is also accompanied by a corresponding decrease in the per prediction power consumption! For this initial Whitepaper, we used a CNN network trained on the Google Speech Commands dataset. We are now actively applying these techniques to larger networks, such as ResNets and Transformers! Stay tuned…..

