A Tale of Two Sparsities: Activation and Weight

Training dense networks requires large numbers of GPUs or TPUs, and can take days or even weeks, resulting in large carbon footprints and spiraling costs. We believe the solution to this problem lies in the brain’s efficiency and power to learn, which arises from sparse connections and activations of neurons. Machine learning has never successfully harnessed sparse activations combined with sparse weights. Together, the two types of sparsity could increase efficiency and drive down the computational cost of neural networks by two orders of magnitude, requiring fewer resources than dense approaches. However, techniques to improve the suitability of sparsity in hardware have compromised accuracy.

To realize sparsity’s potential, Numenta has introduced Complementary Sparsity, a new technology that combines sparse convolution kernels to form a single dense structure. By studying the sparse features of the neocortex and applying what we learned to new architectural solutions, we have implemented sparse-sparse networks that simultaneously leverage weight and activation sparsities. We describe how this approach can be used to efficiently scale machine learning in our new preprint, Two Sparsities Are Better Than One: Unlocking the Performance Benefits of Sparse-Sparse Networks.

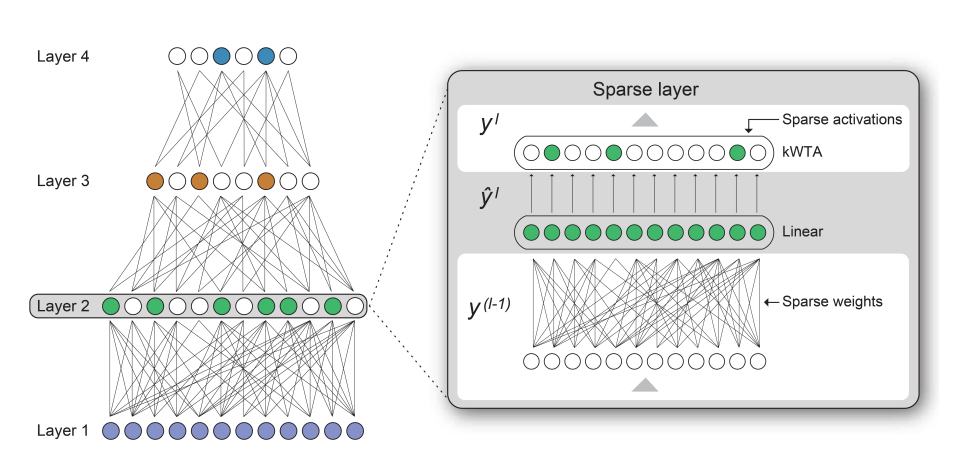
Illustration of our approach to creating a network with sparse activations and sparse weights. A k-winner-takes-all (k-WTA) implementation ensures a consistent quantity of sparse activations for greater efficiency.

Complementary Sparsity—an Architectural Feat

Recent sparse implementations deliver only modest performance benefits using just weight sparsity. Complementary Sparsity overcomes these limitations and delivers a novel architecture solution for sparse-sparse networks on existing hardware. In recently completed tests of Complementary Sparsity, we show over 100X improvement in throughput and energy efficiency performing inference on Field Programmable Gate Arrays (FPGAs). Complementary Sparsity also enables the deployment of DNNs on smaller embedded platforms than previously possible.

To prove the advantages of our approach, we have shown that the techniques scale well and run 30x faster for individual sparse-sparse networks compared to standard dense DNN networks. To prove the feasibility of our approach we also tested scalability and resource tradeoffs using the components of popular networks such as Resnet 50 and MobilNet V2. We found that resource requirements are inversely proportional to sparsity; as sparsity increases so does the efficiency of the network.

In our experiments, this frugal use of resources in sparse-sparse implementations allowed 5X more networks to be accommodated on an FPGA, delivering a full-chip throughput more than 110X higher than the corresponding dense networks. We used our algorithms on Xilinx FPGAs and the Google Speech Commands (GSC) dataset. The demonstration included two off-the-shelf Xilinx FPGAs and Platforms: the Alveo™ U250 and the Zynq™ UltraScale+ ZU3EG. The Alveo U250 is a powerful platform designed for datacenters, while the Zynq class of FPGAs is much smaller and designed for embedded applications.

The Zynq results are particularly promising for applying Complementary Sparsity to embedded platforms.  In many cases, these edge platforms are constrained by limited resources where dense networks do not fit. Complementary Sparsity enables the deployment of DNNs on these resource-restrained platforms.

How Does It Work?

Complementary Sparsity can be used to implement sparse-dense or sparse-sparse networks, reducing the power required and ensuring greater efficiency. Combining multiple sparse weight kernels into a single dense structure, we can implement a sparse-dense architecture that features dense activations and sparse weights. In sparse-dense networks, processing comprises four distinct steps (please see the full preprint to get the broader context):

1. Combine: multiple sparse weight kernels are overlaid to form a single dense structure. This is done offline as a preprocessing step.
2. Multiply: each element of the activation is multiplied by the corresponding weight elements in the dense structure.
3. Route: the appropriate element-wise products are routed separately for each output.
4. Sum: routed products are aggregated and summed to form a separate result for each sparse kernel.

Complementary Sparsity at 80%-sparse packs 5 sparse convolutional kernels — implemented as separate filters with non-zero weights illustrated as the colored squares — into a single dense kernel for processing.

Sparse-Sparse Solutions

For optimal performance, the non-zero activations must be paired with the respective non-zero weights, ensuring all correct weights are paired with activations. Traditional sparse-sparse implementations negate any performance gains due to the overhead associated with locating and pairing non-zero activations with corresponding non-zero weights.

Using Complementary Sparsity, the sparse-sparse problem can now be simplified to a sparse-dense problem, with sparse activations and dense weights. This approach eliminates inefficiencies of sparse-sparse matrix computations due to the changing locations of non-zero elements in the activation vectors. For each sparse (non-zero) activation, our method directs relevant weights to predefined locations in the weight structure, providing for their efficient extraction. Sparse-sparse Complementary Sparsity is comprised of the following five steps:

1. Combine: multiple sparse weight kernels are overlaid to form a single dense structure. This is done offline as a preprocessing step.
2. Select: a k-WTA component is used to determine the top-k activations and their indices.
3. Multiply: each non-zero activation is multiplied by the corresponding weight elements in the dense structure.
4. Route: the appropriate element-wise products are routed separately for each output.
5. Sum: routed products are aggregated and summed to form a separate result for each sparse kernel.

In addition to training a convolutional network on the GSC dataset to recognize one-word speech commands, we implemented dense and sparse versions of the network on both large and small FPGA platforms. This implementation allowed us to study the impact of Complementary Sparsity on words processed per second. The results are shown in the figure below.

The performance comparisons between sparse and dense networks: (a) Sparse network performance on the Xilinx Alveo U250, (b) Sparse-Sparse network performance on the Alveo U250.

What It Means and What’s Next

Complementary Sparsity can be a critical component for efficiently scaling AI over the next decade by essentially inverting the sparsity problem. By structuring sparse matrices in a way where they can be interleaved into a smaller number of dense matrices, we can not only enable high performance weight-sparse networks but gain an additional 3X benefit by simultaneously leveraging activation sparsity. We have already started to broaden our machine learning implementations to include Complementary Sparsity technology.

We are looking beyond convolutional networks at other important architectures. Recently, we implemented sparsity on transformers and are now investigating Complementary Sparsity benefits for this architecture. Our initial investigation of Complementary Sparsity on FPGAs clearly demonstrates its feasibility. We are now investigating application to other key hardware platforms. Beyond inference operations, we also plan to investigate how Complementary Sparsity can be used to accelerate the training of sparse networks.

There’s no question that sparsity in machine learning is becoming increasingly popular. But the question remains: can sparsity leverage the full potential of machine learning and AI without grossly increasing the carbon footprint or driving up requirements for processing power?  Perhaps with one sparsity, the answer is no. But with two sparsities, we believe we can. Complementary Sparsity provides a new way to get us there with greater efficiency!